Motion 1, 三角関数

このエントリーは、アニメーション・モーションを JavaScript で記述するための覚え書きです。いままで実務で使ってきたわざをちょっと整理してみます。
まずは、モーション設計をする上でよく使う三角関数について、おさらいとして触れます。もっともぼくは数学の素養は乏しいので、あやしいところもあるかもしれません。

三角関数おさらい

三角関数を使うと、直角三角形のある角の大きさが定まった時の、各線の長さを求めることができます。

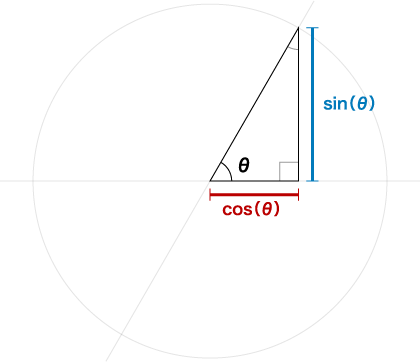
図のように、角度θの時の底辺の長さはsin(θ)、高さはcos(θ)になります。

例えばθが45°の時は
cos(30°) ≓ 0.707
sin(30°) ≓ 0.707（1 : 1 : √2）

60°（上の図）の時は
cos(60°) = 0.5
sin(60°) ≓ 0.8660（1 : 2 : √3 ですね）

90°（垂直線）の時は
cos(90°) = 0
sin(90°) = 1
と、なります。

θに時間軸を与えてsinとcosをグラフに表すと以下のようになります（がんばって canvas 使ってみました）。

ctx.beginPath();
ctx.moveTo( center.x, center.y );
ctx.lineTo( center.x + Math.cos(theta) * radius, center.y + Math.sin(theta) * radius );
ctx.lineTo( center.x + Math.cos(theta) * radius, center.y );
ctx.closePath();
ctx.stroke();

ご覧の通り、斜辺の長さ（radius）が一定であると軌跡が円を描きます。これはとても重要な性質です。三角関数という名前ですが、ぼくとしては円を描くためのツールという印象です。

ちなみに JavaScript で三角関数を求める Math.sin()、Math.cos() の引数には、角度ではなく弧度（radian）を用います。弧度の大きさは、ある角度の円弧の弓の部分の長さと定義されています。全円の円周は 2πr で求めることができるので、全円つまり 360° の弧度は 2π となります。

続く：Motino 2, 円の動き